- ▶
- Heaters/Source
- ▶
- Agilent Heaters and SensorsMass Spectrometry, Scientific Supplies & ManufacturingScientific Instrument Services 5973 Source Heater Tamper Resistant Allen Wrench 5973/5975 Quad Sensor 5985 Source Heater Assembly Agilent Interface Heater Assembly 5971 Interface Heater

- ▶
- LiteratureApplication Notes Adsorbent Resins Guide Mass Spec Tips SDS Sheets FAQ MS Calibration Compound Spectra Manuals MS Links/Labs/ Organizations MS Online Tools Flyers on Products/Services Scientific Supplies Catalog About Us NextAdvance Bullet Blender® Homogenizer Protocols Micro-Mesh® Literature Instrumentation Literature Agilent GC/MS Literature SIS News / E-Mail Newsletter NIST MS Database - Update Notifications

- ▶
- Application NotesNote 103: EPA Method 325B, Novel Thermal Desorption Instrument Modification to Improve Sensitivity Note 102: Identification of Contaminants in Powdered Beverages by Direct Extraction Thermal Desorption GC/MS Note 101: Identification of Contaminants in Powdered Foods by Direct Extraction Thermal Desorption GC/MS Note 100: Volatile and Semi-Volatile Profile Comparison of Whole Versus Cracked Versus Dry Homogenized Barley Grains by Direct Thermal Extraction Note 99: Volatile and Semi-Volatile Profile Comparison of Whole vs. Dry Homogenized Wheat, Rye and Barley Grains by Direct Thermal Extraction GC/MS Note 98: Flavor and Aroma Profiles of Truffle Oils by Thermal Desorption GC/MS Note 97: Flavor Profiles of Imported and Domestic Beers by Purge & Trap Thermal Desorption GC/MS Note 96: Reducing Warping in Mass Spectrometer Filaments, with SISAlloy® Yttria/Rhenium Filaments Note 95: Detection of Explosives on Clothing Material by Direct and AirSampling Thermal Desorption GC/MS Note 94: Detection of Nepetalactone in the Nepeta Cataria Plant by Thermal Desorption GC/MS Note 93: Detection of Benzene in Carbonated Beverages with Purge & Trap Thermal Desorption GC/MS Note 92: Yttria Coated Mass Spectrometer Filaments Note 91: AutoProbe DEP Probe Tip Temperatures Note 90: An Automated MS Direct Probe for use in an Open Access Environment Note 89: Quantitation of Organics via a Mass Spectrometer Automated Direct Probe Note 88: Analysis of Silicone Contaminants on Electronic Components by Thermal Desorption GC-MS Note 87: Design and Development of an Automated Direct Probe for a Mass Spectrometer Note 86: Simulation of a Unique Cylindrical Quadrupole Mass Analyzer Using SIMION 7.0. Note 85: Replacing an Electron Multiplier in the Agilent (HP) 5973 MSD Note 84: Vacuum Pump Exhaust Filters - Charcoal Exhaust Traps Note 83: Vacuum Pump Exhaust Filters - Oil Mist Eliminators Note 82: Vacuum Pump Exhaust Filters Note 81: Rapid Bacterial Chemotaxonomy By DirectProbe/MSD Note 80: Design, Development and Testing of a Microprocessor ControlledAutomated Short Path Thermal Desorption Apparatus Note 79: Volatile Organic Compounds From Electron Beam Cured and Partially Electron Beam Cured Packaging Using Automated Short Path Thermal Desorption Note 78: A New Solution to Eliminate MS Down-Time With No-Tool-Changing of Analytical GC Columns Note 77: The Determination of Volatile Organic Compounds in VacuumSystem Components Note 76: Determination of the Sensitivity of a CRIMS System Note 75: An Apparatus for Sampling Volatile Organics From LivePlant Material Using Short Path Thermal Desorption Note 74: Examination of Source Design in Electrospray-TOF Using SIMION 3D Note 73: The Analysis of Perfumes and their Effect on Indoor Air Pollution Note 72: 1998 Version of the NIST/EPA/NIH Mass Spectral Library, NIST98 Note 71: Flavor Profile Determination of Rice Samples Using Shor tPath Thermal Desorption GC Methods Note 70: Application of SIMION 6.0 To a Study of the Finkelstein Ion Source: Part II Note 69: Application of SIMION 6.0 To a Study of the Finkelstein Ion Source: Part 1 Note 68: Use of a PC Plug-In UV-Vis Spectrometer To Monitor the Plasma Conditions In GC-CRIMS Note 67: Using Chemical Reaction Interface Mass Spectrometry (CRIMS) To Monitor Bacterial Transport In In Situ Bioremediation Note 66: Probe Tip Design For the Optimization of Direct Insertion Probe Performance Note 65: Determination of Ethylene by Adsorbent Trapping and Thermal Desorption - Gas Chromatography Note 64: Comparison of Various GC/MS Techniques For the Analysis of Black Pepper (Piper Nigrum) Note 63: Determination of Volatile and Semi-Volatile Organics in Printer Toners Using Thermal Desorption GC Techniques Note 62: Analysis of Polymer Samples Using a Direct Insertion Probe and EI Ionization Note 61: Analysis of Sugars Via a New DEP Probe Tip For Use With theDirect Probe On the HP5973 MSD Note 60: Programmable Temperature Ramping of Samples Analyzed ViaDirect Thermal Extraction GC/MS Note 59: Computer Modeling of a TOF Reflectron With Gridless Reflector Using SIMION 3D Note 58: Direct Probe Analysis and Identification of Multicomponent Pharmaceutical Samples via Electron Impact MS Note 57: Aroma Profiles of Lavandula species Note 56: Mass Spec Maintenance & Cleaning Utilizing Micro-Mesh® Abrasive Sheets Note 55: Seasonal Variation in Flower Volatiles Note 54: Identification of Volatile Organic Compounds in Office Products Note 53: SIMION 3D v6.0 Ion Optics Simulation Software Note 52: Computer Modeling of Ion Optics in Time-of-Flight mass Spectrometry Using SIMION 3D Note 51: Development and Characterization of a New Chemical Reaction Interface for the Detection of Nonradioisotopically Labeled Analytes Using Mass Spectrometry (CRIMS) Note 50: The Analysis of Multiple Component Drug Samples Using a Direct Probe Interfaced to the HP 5973 MSD Note 49: Analysis of Cocaine Utilizing a New Direct Insertion Probe on a Hewlett Packard 5973 MSD Note 48: Demonstration of Sensitivity Levels For the Detection of Caffeine Using a New Direct Probe and Inlet for the HP 5973 MSD Note 47: The Application Of SIMION 6.0 To Problems In Time-of-Flight Mass Spectrometry Note 46: Delayed Extraction and Laser Desorption: Time-lag Focusing and Beyond Note 45: Application of SIMION 6.0 to Filament Design for Mass Spectrometer Ionization Sources Note 44: The Design Of a New Direct Probe Inlet For a Mass Spectrometer Note 43: Volatile Organic Composition In Blueberries Note 42: The Influence of Pump Oil Purity on Roughing Pumps Note 41: Hydrocarbon Production in Pine by Direct Thermal Extraction Note 40: Comparison of Septa by Direct Thermal Extraction Note 39: Comparison of Sensitivity Of Headspace GC, Purge and Trap Thermal Desorption and Direct Thermal Extraction Techniques For Volatile Organics Note 38: A New Micro Cryo-Trap For Trapping Of Volatiles At the Front Of a GC Capillary Column Note 37: Volatile Organic Emissions from Automobile Tires Note 36: Identification Of Volatile Organic Compounds In a New Automobile Note 35: Volatile Organics Composition of Cranberries Note 34: Selection Of Thermal Desorption and Cryo-Trap Parameters In the Analysis Of Teas Note 33: Changes in Volatile Organic Composition in Milk Over Time Note 32: Selection and Use of Adsorbent Resins for Purge and Trap Thermal Desorption Applications Note 31: Volatile Organic Composition in Several Cultivars of Peaches Note 30: Comparison Of Cooking Oils By Direct Thermal Extraction and Purge and Trap GC/MS Note 29: Analysis Of Volatile Organics In Oil Base Paints By Automated Headspace Sampling and GC Cryo-Focusing Note 28: Analysis Of Volatile Organics In Latex Paints By Automated Headspace Sampling and GC Cryo-Focusing Note 27: Analysis of Volatile Organics In Soils By Automated Headspace GC Note 26: Volatile Organics Present in Recycled Air Aboard a Commercial Airliner Note 25: Flavor and Aroma in Natural Bee Honey Note 24: Selection of GC Guard Columns For Use With the GC Cryo-Trap Note 23: Frangrance Qualities in Colognes Note 22: Comparison Of Volatile Compounds In Latex Paints Note 21: Detection and Identification Of Volatile and Semi-Volatile Organics In Synthetic Polymers Used In Food and Pharmaceutical Packaging Note 20: Using Direct Thermal Desorption to Assess the Potential Pool of Styrene and 4-Phenylcyclohexene In Latex-Backed Carpets Note 19: A New Programmable Cryo-Cooling/Heating Trap for the Cryo-Focusing of Volatiles and Semi-Volatiles at the Head of GC Capillary Columns Note 18: Determination of Volatile Organic Compounds In Mushrooms Note 17: Identification of Volatile Organics in Wines Over Time Note 16: Analysis of Indoor Air and Sources of Indoor Air Contamination by Thermal Desorption Note 14: Identification of Volatiles and Semi-Volatiles In Carbonated Colas Note 13: Identification and Quantification of Semi-Volatiles In Soil Using Direct Thermal Desorption Note 12: Identification of the Volatile and Semi-Volatile Organics In Chewing Gums By Direct Thermal Desorption Note 11: Flavor/Fragrance Profiles of Instant and Ground Coffees By Short Path Thermal Desorption Note 10: Quantification of Naphthalene In a Contaminated Pharmaceutical Product By Short Path Thermal Desorption Note 9: Methodologies For the Quantification Of Purge and Trap Thermal Desorption and Direct Thermal Desorption Analyses Note 8: Detection of Volatile Organic Compounds In Liquids Utilizing the Short Path Thermal Desorption System Note 7: Chemical Residue Analysis of Pharmaceuticals Using The Short Path Thermal Desorption System Note 6: Direct Thermal Analysis of Plastic Food Wraps Using the Short Path Thermal Desorption System Note 5: Direct Thermal Analysis Using the Short Path Thermal Desorption System Note 4: Direct Analysis of Spices and Coffee Note 3: Indoor Air Pollution Note 2: Detection of Arson Accelerants Using Dynamic Headspace with Tenax® Cartridges Thermal Desorption and Cryofocusing Note 1: Determination of Off-Odors and Other Volatile Organics In Food Packaging Films By Direct Thermal Analysis-GC-MS Tech No. "A" Note 14: Elimination of "Memory" Peaks in Thermal Desorption Improving Sensitivity in the H.P. 5971 MSD and Other Mass Spectrometers - Part I of II Improving Sensitivity in the H.P. 5971 MSD and Other Mass Spectrometers- Part II of II Adsorbent Resins Guide Development and Field Tests of an Automated Pyrolysis Insert for Gas Chromatography. Hydrocarbon Production in Pine by Direct Thermal Extraction A New Micro Cryo-Trap for the Trapping of Volatiles at the Front of a GC Capillary (019P) - Comparison of Septa by Direct Thermal Extraction Volatile Organic Composition in Blueberry Identification of Volatile Organic Compounds in Office Products Detection and Indentification of Volatiles in Oil Base Paintsby Headspace GC with On Column Cryo-Trapping Evaluation of Septa Using a Direct Thermal Extraction Technique INFLUENCE OF STORAGE ON BLUEBERRY VOLATILES Selection of Thermal Desorption and Cryo-Trap Parameters in the Analysis of Teas Redesign and Performance of a Diffusion Based Solvent Removal Interface for LC/MS The Design of a New Direct Probe Inlet for a Mass Spectrometer Analytes Using Mass Spectrometry (CRIMS) Application of SIMION 6.0 to Filament Design for Mass Spectrometer Ionization Sources A Student Guide for SIMION Modeling Software Application of SIMION 6.0 to Problems in Time-of-flight Mass Spectrometry Comparison of Sensitivity of Headspace GC, Purge and TrapThermal Desorption and Direct Thermal Extraction Techniques forVolatile Organics The Influence of Pump Oil Purity on Roughing Pumps Analysis of Motor Oils Using Thermal Desorption-Gas Chromatography-Mass Spectrometry IDENTIFICATION OF VOLATILE ORGANIC COMPOUNDS IN PAPER PRODUCTS Computer Modeling of Ion Optics in Time-of-Flight mass Spectrometry using SIMION 3D Seasonal Variation in Flower Volatiles Development of and Automated Microprocessor Controlled Gas chromatograph Fraction Collector / Olfactometer Delayed Extraction and Laser Desorption: Time-lag Focusing and Beyond A New Micro Cryo-Trap for the Trapping of Volatiles at the Front of a GC Column Design of a Microprocessor Controlled Short Path Thermal Desorption Autosampler Computer Modeling of Ion Optics in Time-of-Flight Mass Spectrometry Using SIMION 3D Thermal Desorption Instrumentation for Characterization of Odors and Flavors

- ▶
- Note 46: Delayed Extraction and Laser Desorption: Time-lag Focusing and Beyond (This Page)
1999
INTRODUCTION
Recent experiments have shown that the proper use of delayed ion extraction can dramatically improve the mass resolution of laser desorption time-of-flight mass spectrometry (LD-TOFMS) [1-4]. This poster explores two algorithms for the identification of optimal instrumental parameters in these experiments. The first, described in Wiley and McLaren's 1955 paper, is an analytical approach that has been in use for over 40 years [5]. The second, space-velocity correlation focusing, is a recently published computational method that depends on numerical optimization techniques to determine instrumental parameters [6]. Both approaches are used to calculate conditions in which the same physical phenomenon results in improved mass resolution. Wiley and McLaren's calculations were described for a system in which ionization occurred in the gas phase. We now consider the validity of the assumptions made in each approach when they are applied to surface desorption.
Time-lag Focusing
In their landmark 1955 paper [5], Wiley and McLaren described two focusing techniques for time-of-flight mass spectrometry, space and time-lag focusing. Both of these methods were applicable to ions generated in the gas phase. Space focusing was used to minimize peak broadening due to the spatial distribution of ions at the beginning of the time-of-flight measurement. Instrument operating conditions were identified by taking the derivative of an equation for an ion's time-of-flight with respect to the initial position. This derivative was then set equal to zero in order to minimize the spatial dependence of flight time (T). (dT/dX0=0, where X0 is the average position at the start of the time measurement.) By supplying a value for X0, one can calculate the best ratio for the fields in the two acceleration regions of the source. The desired drift energy is then used to establish acceleration voltages in the instrument. An important assumption in this method is that dT/dX0 does not vary significantly over the range of the spatial distribution of the sample.
Time-lag focusing employs a time delay between the formation of ions and their (time delayed) extraction from the source to reduce the impact of the analyte's initial velocity distribution on the detected peak width. During the delay time, (t) ions move to new positions as a function of their nascent velocities. When the extraction potential is applied, ions with velocities towards the detector will have moved to regions of lower potential energies and those traveling away from the detector will find themselves at a greater potential. Under the proper conditions, the change in potential energy can compensate for the differences in initial velocity. Wiley and McLaren point out that during the time (t) ions will move a distance v0(t) where v0 is the initial velocity along the coordinate of interest. This will result in a flight time change of approximately (dT/dX0)v0t. Without a delay, the flight time difference between ions of velocity v0 and 0 is approximately "one-half turn-around time" or mv0/qE1. Where m is the mass, q is the charge, and E1 is the electric field after the extraction voltage is applied. (In their version of this equation, Wiley and McLaren included a factor of 1.02 for unit conversion). Although not explained in the 1955 paper, this equation is derived by taking the derivative dT/dv0 and assuming the average initial velocity equals zero. Focusing conditions are found when the change in flight time due to the delay compensates for the differences in flight time expected from the various kinetic energies, i.e. (dT/dX0)v0t= -dT/dv0. This is expressed as:
![]() (Reference
5 Equation 13)
(Reference
5 Equation 13)
in Wiley and McLaren's paper and rearranged to
![]() (Reference
5 Equation 13a)
(Reference
5 Equation 13a)
in order to calculate the proper time delay t.
There are a number of assumptions made in Wiley and McLaren's derivation of this equation. dT/dX0 and dT/dv0 are assumed to be relatively constant over the ranges of interest. dT/dX0 not only needs to be uniform over the volume in which ions are produced but also over the distances represented by v0t. The derivation also assumes that the average value of v0 be equal to zero. This was done in the calculation of the derivative dT/dv0 = mv0/qE1 and results in an equation that is independent of v0. Finally, one must choose a value of X0 in order to calculate dT/dX0. Thus a single X0 is assumed to represent the positions of all of the ions.
The recommended implementation of time-lag focusing involves the selection of space-focusing conditions followed by the variation of a parameter such that dT/dX0 becomes negative. This violates the space focusing criteria and Wiley and McLaren therefore stress that space focusing and time-lag focusing are mutually exclusive. "The t and dT/dX0 combination yielding the best overall resolution is a compromise between two extremes." If t is very small then dT/dX0 must be large and space resolution becomes the limiting factor. If t is too large, ions travel over a range where dT/dX0 is not sufficiently constant. Consequently, a value of t cannot be calculated under conditions where space focusing has been used to determine the grid potentials. No criteria are given for the selection of which parameter to vary in order to make the derivative negative. Optimum conditions must therefore be found using a certain amount of trial and error.
The Application of Time-Lag Focusing to Samples Desorbed From a Surface
In most laser desorption techniques (e.g. MALDI), a broad initial velocity distribution is presumed to be a major factor leading to reduced mass resolution. However, it is clear that the time-lag focusing algorithm, as described by Wiley and McLaren, cannot be applied directly to this problem. This is due to the non-zero value for the average initial velocity. Fortunately, it is possible to change their approach and remove the assumption that v0 equals zero. In this case the equation for the derivative dT/dv0 is:
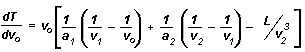
where ax is the acceleration in each region, v1 and v2 are the velocities after the first two regions, and L is the length of the drift region. A value for t could now be calculated given values for X0, v , voltages, and distances. However, it is also necessary to examine the validity of the other assumptions involved in the Wiley and McLaren approach.
The first assumptions discussed above are that the values of dT/dX0 and dT/dv0 are uniform over the spatial and velocity distributions of the ions. (Note that the spatial distribution we are concerned with is that found at the time of ion extraction not just that present at the moment of ionization.) The assumptions can be studied by examining plots of flight time verses initial position or initial velocity. Three previously published examples [2] are shown in Figure 1. These plots show data for an ion of m/z=23981 calculated using different values for the potentials of the extraction voltages. In each case the value of t has been optimized. Note that the x-axis could be labeled in either velocity or position at any given value of t, because the two variables are correlated by the simple equation X0 = v0t when the sample is desorbed from a surface. Since all ions start in approximately the same place, v0t may be used to represent position-not just displacement as was done by Wiley and McLaren. The initial velocity range that we must be concerned with has been experimentally determined by a number of workers [7-11] and is approximately 750 +/- 500 m/s. It is clear that dT/dX0 and dT/dv0 (the slopes of the curves in Figure 1) vary substantially over this range. They are even found to change sign. The variation is greatest when several minima and maxima occur as in Figure 1C. This is a particular problem, since this third order structure is indicative of the best extraction potentials.
In order to calculate a value for t, using Wiley and McLaren's approach one assumes that there is a single value of X0 that adequately represents all of the ions. When the sample is desorbed from a surface, one must also select a value for v0, since dT/dv0 is no longer independent of the initial velocity. Figure 1C shows how critical the selection of these variables are. For example, the values of dT/dX0 and dT/dv0 change substantially between 850 and 950 m/s. It is disconcerting to know that a small change in the chosen value of v0 will make a dramatic difference in the calculated value of t, particularly when the range of v0 is known to be large. This suggests that the calculated t will properly focus only a small fraction of the ions. The selection of X0 presents an additional problem. X0 should be approximately related to v0 by the relation X0 = v0t. However, a value of t is needed to solve this equation and t cannot be calculated until X0 is known.
Using the approach of Wiley and McLaren, the implementation of time-lag focusing to desorbed samples would involve the selection of space-focusing conditions and then changing a parameter such that dT/dX0 becomes negative. However, space focusing conditions cannot be determined until X0 is known, which in turn requires t. The requirement that dT/dX0 be negative is also questionable for surface desorption. Figure 1 illustrates several examples where t is optimized, but a positive slope can be found for any probable value of v0. Figure 1 also shows the importance of optimizing instrumental parameters other than t. Each plot was produced with conditions for which t was optimized but other potentials were differed. However, the range of calculated flight times is clearly much narrower in Figure 1C. Wiley and McLaren provide no criteria for the selection of parameters other than t except to suggest that one start with space focusing conditions.
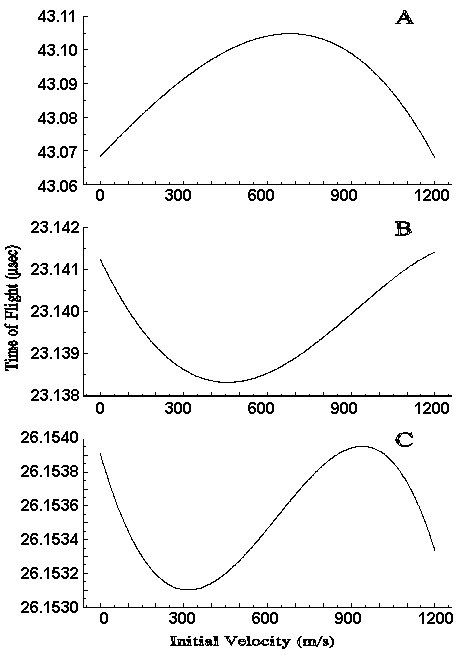
Figure 1. Calculated Flight Times As a Function Of Initial Velocity (and position) for various instrumental conditions. The delay time (t) has been optimized in all cases.
Space-Velocity Correlation Focusing (SVCF)
SVCF is an alternative method for determining delayed extraction conditions. It is a numerical process in which iterative calculations are used to optimize instrumental parameters [6]. The algorithm is called Space-Velocity Correlation Focusing, because it takes advantage of correlation between the distributions of ion positions and velocities at the time of extraction. Briefly, the approach involves finding a relationship between the two distributions, using the resulting expression to eliminate a variable (X0 or v0) from the equation for ion time-of-flight and then calculating flight times as a function of the remaining variable. The results can be used to produce plots such as those shown in Figure 1. With these, one can examine the flight time spread expected as a result of the remaining variable. This spread is then used as a figure of merit for the optimization of instrumental parameters, such as, but not restricted to, the delay time t. Optimization may then be accomplished by simple parameter variation or by any of a variety of established numerical optimization routines (i. e. Simplex). Since the two distributions are related, both spatial and velocity focusing can be accomplished simultaneously.
SVCF has a number of advantages over the time-lag focusing algorithm presented in 1955. In particular, it involves none of the assumptions discussed above and can be used to optimize any or all of the instrumental parameters. These are the most important factors differentiating it from time-lag focusing. SVCF does, however, require other assumptions. Foremost among these is the presupposition that the spatial and velocity distributions at the time of extraction are the primary factors limiting resolution. Other possible contributions such as metastable decay have not yet been included in the model. One must also select a range of initial velocities (or positions) over which focusing is to be calculated. Although this is preferred over picking a single velocity, as in time-lag focusing, the proper choice of values is still important to the results obtained. Finally, the approach requires that a relationship between the initial spatial and velocity distributions can be found that is valid for the relevant range of conditions. Typically, a simple analytical relation such as X0 = v0t has been used to represent this dependence. It requires that all ions are formed in the same location, do not fragment, and do not undergo collisions that change their velocity. These assumptions, made in the dynamic environment of the desorption, are more tenuous than those made when v0t is used to represent the distance an ion moves in the gas phase as is done in time-lag focusing [11]. Fortunately, if the distributions can be measured, they can be incorporated in the SVCF approach either numerically or as an analytical expression. A full description of the implementation of SVCF is presented in Reference 6.
Conclusion
We have examined two methods for calculating optimum conditions in delayed
extraction TOFMS. The assumptions required in each are summarized in Table
1. It is clear that the application of Wiley and McLaren's time-lag focusing
algorithum to samples desorbed from a surface must be made with caution.
Many of the assumptions made in this approach are questionable when the
sample does not originate in the gas phase. In addition, it is clear that
it is not sufficient to optimize only the extraction delay. Other instrumental
parameters are critical to the mass resolution attained. While the time-lag
focusing algorithm has been used for many years, these factors prevented
the full benefit of delayed extraction of desorbed samples from being realized
until 1994 [1-3]. In contrast, the SVCF approach requires fewer assumptions
and may be applied to a larger variety of experimental conditions. SVCF
is, however, more complicated than time-lag focusing. It also involves
a variety of iterative calculations that are best performed on a computer.
We suggest that one carefully consider the limitations of both of these
methods when determining optimal conditions for delayed extraction TOFMS.
| Time-lag Focusing | Space-Velocity Correlation Focusing |
| Initial spatial and velocity distributions are the primary factors limiting resolution. | Initial spatial and velocity distributions are the primary factors limiting resolution. |
| dT/dX0 and dT/dv0 are constant over applicable ranges. | dT/dX0 and dT/dv0 may take any values over the applicable ranges. |
| A single value of X0 represents all ions. | A range of X0 values represents all ions. |
| Average v0 equals zero, or, if the method is extended, a single value of v0 represents all ions. | A range of positive v0 values represents all ions. |
| X0 is approximated before t is known. | No approximations are needed. |
| dT/dX0 must be negative. | dT/dX0 may be positive, zero, or negative. |
| Variables other then t can be optimized by trial & error. | All parameters may be optimized through a well defined algorithm. |
| Ions are formed over a spatial volume represented by a single value of X0. | Ions are formed in a small volume such that some relationship, such as X0 = v0t, is a good approximation. |
| Initial distributions do not need to be related. | Initial distributions are related by a quantifiable dependence. (i.e. X0 = v0t) |
| Collisions do not affect the distance ions travel during the delay time. | Collisions do not invalidate the stated dependence between distributions. |
| Metastable decay does not occur during the delay time. | Metastable decay do not invalidate the stated dependence. |
References
1. Brown, R. S.; Lennon, J. J.; Christie, D. Desorption '94, Sunriver Lodge, OR, March 27-31, 1994, p. 63. and Lennon, J. J.; Brown, R. S. 42nd ASMS Conf. On Mass Spectrom. 1994, 501. And Brown R. S. and Lennon J. J.; Anal. Chem. 1995, 67, 1998-2003.
2. Colby, S. M.; King, T. B.; Reilly, J. P. Rapid Commun. Mass Spectrom. 1994, 8, 865-868.
3. Whittal, R. M.; Li, L. Anal. Chem. 1995, 67, 1950-1954.
4. Vestal, M. L.; Juhasz, P.; Martin, S. A. Rapid Commun. Mass Spectrom. 1995, 9, 1044-1050.
5. Wiley, W. C.; McLaren I. H. Rev. Sci. Instrum. 1955, 26, 1150-1157.
6. Colby, S. M.; Reilly, J. P. Anal. Chem. 1996, 68, 1419-1428. U.S. Patents 5,504,326; 5,510,613.
7. Beavis, R. C.; Chait, B. T. Chem. Phys. Lett. 1991, 181 (5), 479-484.
8. Huth-Fehre, T.; Becker, C. H. Rapid Commun. Mass Spectrom. 1991, 5, 378-382.
9. Chan, T.-W. D.; Thomas, I.; Colburn, A. W.; Derrick, P. J. Chem. Phys. Lett. 1994, 222, 579-585.
10. Zhou, J.; Ens, W.; Standing, K. G.; Verentchikov, A. Rapid Commun. Mass Spectrom. 1992, 6, 671-678.
11. King, R. C.; Owens, K. G. 41st ASMS Conf. On Mass Spectrom. 1993, 778. and 42nd ASMS Conf. On Mass Spectrom. 1994.

