- ▶
- Heaters/Source
- ▶
- Agilent Heaters and SensorsMass Spectrometry, Scientific Supplies & ManufacturingScientific Instrument Services 5973 Source Heater Tamper Resistant Allen Wrench 5973/5975 Quad Sensor 5985 Source Heater Assembly Agilent Interface Heater Assembly 5971 Interface Heater

- ▶
- LiteratureApplication Notes Adsorbent Resins Guide Mass Spec Tips SDS Sheets FAQ MS Calibration Compound Spectra Manuals MS Links/Labs/ Organizations MS Online Tools Flyers on Products/Services Scientific Supplies Catalog About Us NextAdvance Bullet Blender® Homogenizer Protocols Micro-Mesh® Literature Instrumentation Literature Agilent GC/MS Literature SIS News / E-Mail Newsletter NIST MS Database - Update Notifications

- ▶
- Application NotesNote 103: EPA Method 325B, Novel Thermal Desorption Instrument Modification to Improve Sensitivity Note 102: Identification of Contaminants in Powdered Beverages by Direct Extraction Thermal Desorption GC/MS Note 101: Identification of Contaminants in Powdered Foods by Direct Extraction Thermal Desorption GC/MS Note 100: Volatile and Semi-Volatile Profile Comparison of Whole Versus Cracked Versus Dry Homogenized Barley Grains by Direct Thermal Extraction Note 99: Volatile and Semi-Volatile Profile Comparison of Whole vs. Dry Homogenized Wheat, Rye and Barley Grains by Direct Thermal Extraction GC/MS Note 98: Flavor and Aroma Profiles of Truffle Oils by Thermal Desorption GC/MS Note 97: Flavor Profiles of Imported and Domestic Beers by Purge & Trap Thermal Desorption GC/MS Note 96: Reducing Warping in Mass Spectrometer Filaments, with SISAlloy® Yttria/Rhenium Filaments Note 95: Detection of Explosives on Clothing Material by Direct and AirSampling Thermal Desorption GC/MS Note 94: Detection of Nepetalactone in the Nepeta Cataria Plant by Thermal Desorption GC/MS Note 93: Detection of Benzene in Carbonated Beverages with Purge & Trap Thermal Desorption GC/MS Note 92: Yttria Coated Mass Spectrometer Filaments Note 91: AutoProbe DEP Probe Tip Temperatures Note 90: An Automated MS Direct Probe for use in an Open Access Environment Note 89: Quantitation of Organics via a Mass Spectrometer Automated Direct Probe Note 88: Analysis of Silicone Contaminants on Electronic Components by Thermal Desorption GC-MS Note 87: Design and Development of an Automated Direct Probe for a Mass Spectrometer Note 86: Simulation of a Unique Cylindrical Quadrupole Mass Analyzer Using SIMION 7.0. Note 85: Replacing an Electron Multiplier in the Agilent (HP) 5973 MSD Note 84: Vacuum Pump Exhaust Filters - Charcoal Exhaust Traps Note 83: Vacuum Pump Exhaust Filters - Oil Mist Eliminators Note 82: Vacuum Pump Exhaust Filters Note 81: Rapid Bacterial Chemotaxonomy By DirectProbe/MSD Note 80: Design, Development and Testing of a Microprocessor ControlledAutomated Short Path Thermal Desorption Apparatus Note 79: Volatile Organic Compounds From Electron Beam Cured and Partially Electron Beam Cured Packaging Using Automated Short Path Thermal Desorption Note 78: A New Solution to Eliminate MS Down-Time With No-Tool-Changing of Analytical GC Columns Note 77: The Determination of Volatile Organic Compounds in VacuumSystem Components Note 76: Determination of the Sensitivity of a CRIMS System Note 75: An Apparatus for Sampling Volatile Organics From LivePlant Material Using Short Path Thermal Desorption Note 74: Examination of Source Design in Electrospray-TOF Using SIMION 3D Note 73: The Analysis of Perfumes and their Effect on Indoor Air Pollution Note 72: 1998 Version of the NIST/EPA/NIH Mass Spectral Library, NIST98 Note 71: Flavor Profile Determination of Rice Samples Using Shor tPath Thermal Desorption GC Methods Note 70: Application of SIMION 6.0 To a Study of the Finkelstein Ion Source: Part II Note 69: Application of SIMION 6.0 To a Study of the Finkelstein Ion Source: Part 1 Note 68: Use of a PC Plug-In UV-Vis Spectrometer To Monitor the Plasma Conditions In GC-CRIMS Note 67: Using Chemical Reaction Interface Mass Spectrometry (CRIMS) To Monitor Bacterial Transport In In Situ Bioremediation Note 66: Probe Tip Design For the Optimization of Direct Insertion Probe Performance Note 65: Determination of Ethylene by Adsorbent Trapping and Thermal Desorption - Gas Chromatography Note 64: Comparison of Various GC/MS Techniques For the Analysis of Black Pepper (Piper Nigrum) Note 63: Determination of Volatile and Semi-Volatile Organics in Printer Toners Using Thermal Desorption GC Techniques Note 62: Analysis of Polymer Samples Using a Direct Insertion Probe and EI Ionization Note 61: Analysis of Sugars Via a New DEP Probe Tip For Use With theDirect Probe On the HP5973 MSD Note 60: Programmable Temperature Ramping of Samples Analyzed ViaDirect Thermal Extraction GC/MS Note 59: Computer Modeling of a TOF Reflectron With Gridless Reflector Using SIMION 3D Note 58: Direct Probe Analysis and Identification of Multicomponent Pharmaceutical Samples via Electron Impact MS Note 57: Aroma Profiles of Lavandula species Note 56: Mass Spec Maintenance & Cleaning Utilizing Micro-Mesh® Abrasive Sheets Note 55: Seasonal Variation in Flower Volatiles Note 54: Identification of Volatile Organic Compounds in Office Products Note 53: SIMION 3D v6.0 Ion Optics Simulation Software Note 52: Computer Modeling of Ion Optics in Time-of-Flight mass Spectrometry Using SIMION 3D Note 51: Development and Characterization of a New Chemical Reaction Interface for the Detection of Nonradioisotopically Labeled Analytes Using Mass Spectrometry (CRIMS) Note 50: The Analysis of Multiple Component Drug Samples Using a Direct Probe Interfaced to the HP 5973 MSD Note 49: Analysis of Cocaine Utilizing a New Direct Insertion Probe on a Hewlett Packard 5973 MSD Note 48: Demonstration of Sensitivity Levels For the Detection of Caffeine Using a New Direct Probe and Inlet for the HP 5973 MSD Note 47: The Application Of SIMION 6.0 To Problems In Time-of-Flight Mass Spectrometry Note 46: Delayed Extraction and Laser Desorption: Time-lag Focusing and Beyond Note 45: Application of SIMION 6.0 to Filament Design for Mass Spectrometer Ionization Sources Note 44: The Design Of a New Direct Probe Inlet For a Mass Spectrometer Note 43: Volatile Organic Composition In Blueberries Note 42: The Influence of Pump Oil Purity on Roughing Pumps Note 41: Hydrocarbon Production in Pine by Direct Thermal Extraction Note 40: Comparison of Septa by Direct Thermal Extraction Note 39: Comparison of Sensitivity Of Headspace GC, Purge and Trap Thermal Desorption and Direct Thermal Extraction Techniques For Volatile Organics Note 38: A New Micro Cryo-Trap For Trapping Of Volatiles At the Front Of a GC Capillary Column Note 37: Volatile Organic Emissions from Automobile Tires Note 36: Identification Of Volatile Organic Compounds In a New Automobile Note 35: Volatile Organics Composition of Cranberries Note 34: Selection Of Thermal Desorption and Cryo-Trap Parameters In the Analysis Of Teas Note 33: Changes in Volatile Organic Composition in Milk Over Time Note 32: Selection and Use of Adsorbent Resins for Purge and Trap Thermal Desorption Applications Note 31: Volatile Organic Composition in Several Cultivars of Peaches Note 30: Comparison Of Cooking Oils By Direct Thermal Extraction and Purge and Trap GC/MS Note 29: Analysis Of Volatile Organics In Oil Base Paints By Automated Headspace Sampling and GC Cryo-Focusing Note 28: Analysis Of Volatile Organics In Latex Paints By Automated Headspace Sampling and GC Cryo-Focusing Note 27: Analysis of Volatile Organics In Soils By Automated Headspace GC Note 26: Volatile Organics Present in Recycled Air Aboard a Commercial Airliner Note 25: Flavor and Aroma in Natural Bee Honey Note 24: Selection of GC Guard Columns For Use With the GC Cryo-Trap Note 23: Frangrance Qualities in Colognes Note 22: Comparison Of Volatile Compounds In Latex Paints Note 21: Detection and Identification Of Volatile and Semi-Volatile Organics In Synthetic Polymers Used In Food and Pharmaceutical Packaging Note 20: Using Direct Thermal Desorption to Assess the Potential Pool of Styrene and 4-Phenylcyclohexene In Latex-Backed Carpets Note 19: A New Programmable Cryo-Cooling/Heating Trap for the Cryo-Focusing of Volatiles and Semi-Volatiles at the Head of GC Capillary Columns Note 18: Determination of Volatile Organic Compounds In Mushrooms Note 17: Identification of Volatile Organics in Wines Over Time Note 16: Analysis of Indoor Air and Sources of Indoor Air Contamination by Thermal Desorption Note 14: Identification of Volatiles and Semi-Volatiles In Carbonated Colas Note 13: Identification and Quantification of Semi-Volatiles In Soil Using Direct Thermal Desorption Note 12: Identification of the Volatile and Semi-Volatile Organics In Chewing Gums By Direct Thermal Desorption Note 11: Flavor/Fragrance Profiles of Instant and Ground Coffees By Short Path Thermal Desorption Note 10: Quantification of Naphthalene In a Contaminated Pharmaceutical Product By Short Path Thermal Desorption Note 9: Methodologies For the Quantification Of Purge and Trap Thermal Desorption and Direct Thermal Desorption Analyses Note 8: Detection of Volatile Organic Compounds In Liquids Utilizing the Short Path Thermal Desorption System Note 7: Chemical Residue Analysis of Pharmaceuticals Using The Short Path Thermal Desorption System Note 6: Direct Thermal Analysis of Plastic Food Wraps Using the Short Path Thermal Desorption System Note 5: Direct Thermal Analysis Using the Short Path Thermal Desorption System Note 4: Direct Analysis of Spices and Coffee Note 3: Indoor Air Pollution Note 2: Detection of Arson Accelerants Using Dynamic Headspace with Tenax® Cartridges Thermal Desorption and Cryofocusing Note 1: Determination of Off-Odors and Other Volatile Organics In Food Packaging Films By Direct Thermal Analysis-GC-MS Tech No. "A" Note 14: Elimination of "Memory" Peaks in Thermal Desorption Improving Sensitivity in the H.P. 5971 MSD and Other Mass Spectrometers - Part I of II Improving Sensitivity in the H.P. 5971 MSD and Other Mass Spectrometers- Part II of II Adsorbent Resins Guide Development and Field Tests of an Automated Pyrolysis Insert for Gas Chromatography. Hydrocarbon Production in Pine by Direct Thermal Extraction A New Micro Cryo-Trap for the Trapping of Volatiles at the Front of a GC Capillary (019P) - Comparison of Septa by Direct Thermal Extraction Volatile Organic Composition in Blueberry Identification of Volatile Organic Compounds in Office Products Detection and Indentification of Volatiles in Oil Base Paintsby Headspace GC with On Column Cryo-Trapping Evaluation of Septa Using a Direct Thermal Extraction Technique INFLUENCE OF STORAGE ON BLUEBERRY VOLATILES Selection of Thermal Desorption and Cryo-Trap Parameters in the Analysis of Teas Redesign and Performance of a Diffusion Based Solvent Removal Interface for LC/MS The Design of a New Direct Probe Inlet for a Mass Spectrometer Analytes Using Mass Spectrometry (CRIMS) Application of SIMION 6.0 to Filament Design for Mass Spectrometer Ionization Sources A Student Guide for SIMION Modeling Software Application of SIMION 6.0 to Problems in Time-of-flight Mass Spectrometry Comparison of Sensitivity of Headspace GC, Purge and TrapThermal Desorption and Direct Thermal Extraction Techniques forVolatile Organics The Influence of Pump Oil Purity on Roughing Pumps Analysis of Motor Oils Using Thermal Desorption-Gas Chromatography-Mass Spectrometry IDENTIFICATION OF VOLATILE ORGANIC COMPOUNDS IN PAPER PRODUCTS Computer Modeling of Ion Optics in Time-of-Flight mass Spectrometry using SIMION 3D Seasonal Variation in Flower Volatiles Development of and Automated Microprocessor Controlled Gas chromatograph Fraction Collector / Olfactometer Delayed Extraction and Laser Desorption: Time-lag Focusing and Beyond A New Micro Cryo-Trap for the Trapping of Volatiles at the Front of a GC Column Design of a Microprocessor Controlled Short Path Thermal Desorption Autosampler Computer Modeling of Ion Optics in Time-of-Flight Mass Spectrometry Using SIMION 3D Thermal Desorption Instrumentation for Characterization of Odors and Flavors

- ▶
- Note 47: The Application Of SIMION 6.0 To Problems In Time-of-Flight Mass Spectrometry (This Page)
1999
INTRODUCTION
This poster examines the use of SIMION 3D v.6.0 in Time-of-Flight Mass Spectrometry. SIMION is a ion optics software program originally developed by David Dahl at the Idaho National Laboratory.1 The latest version allows for greatly expanded simulation capabilities. These include larger array size (10 million points) and three dimensional modeling. Dynamic parameter variation and time varying potentials are now also possible.
We use two examples to show how the software can be used to analyze and solve problems in Time-of-Flight Mass Spectrometry. These involve the proper use of Einzel lenses and the effects of non-ideal grids. The simulation of Einzel lenses examines the effects of lens polarity on the time-of-flight distribution of the ions. Our examination of non-ideal grids illustrates the deflection of ions and quantifies the effects of different grid types.
Effects Of Einzel Lenses In Time-of-Flight Mass Spectrometry
Einzel lenses are a common tool in TOFMS. They are often used to focus ions to the detector and thereby improve sensitivity. The need for focusing increases with the length of the instrument and the fraction of kinetic energy perpendicular to the path toward the detector. A typical Einzel lens is shown in Figure 1. It consists of three electrode elements. The outer two are held at the same potential, typically ground, while the center is held at a potential appropriate for the desired focusing. It is possible to focus both positive and negative ions with either positive or negative potentials on the center electrode. However, the choice of polarity can markedly affect the time-of-flight distribution of the ions at the focal point.
Fig. 1 - Trajectories Of Ions Passing Thru an Einzel Lens

Simulation
We have used SIMION 3D to model the Einzel lens shown in Figure 1. (A section is cut away to show the passage of ions.) The optic was 36mm long with an inner diameter of 14.2mm. Two focusing scenarios were examined. The first involved ions originating along a line 80 mm from the lens and focused to a point 300 mm from their source. (Figure 1). The second looked at ions coming from a point and focused within an 18 mm diameter target. Distances were the same in both cases. Ions were always considered to be positive and to have 200 eV of energy. SIMION's potential adjustment was used to optimize focusing voltages. It was a simple matter to identify both the positive and negative optimal focusing values for each scenario. It should be noted that complicated optimization routines may be developed using SIMION's user programming interface. This tool may be used, for instance, to choose the best grid voltages in a TOF reflectron.
Results and Conclusions
Figure 2A summarizes the results obtained when ions started from a line perpendicular to their flight. Optimal focusing potentials were found at +40.0 and -62.0V. As seen in the figure the flight times calculated using either voltage range over a number of nanoseconds. These ranges were 26.7 and 41.6 ns for the negative and positive potentials respectively. The two parabolic shapes are due to the accelerating or decelerating effects of the center electrode. Those ions that pass closest to the electrode surface are most strongly affected.
Fig. 2 - Ion Flight Times As a Function Of Lens Polarity and Ion Position
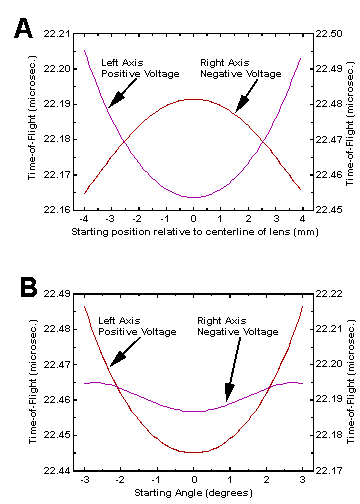
The results obtained when ions originated from a point are shown in Figure 2B. The data were generated using the optimum potentials of +38.0 and -65.3V. The difference in flight time ranges was even more pronounced. These were calculated to be 41.4 and 8.1 ns, respectively. These values clearly show the importance of selecting the correct voltage polarity.
The results presented above demonstrate the advantage of using SIMION to examine ion optics in TOFMS. The results shown apply to a specific geometry, but one can make the general conclusion that it is preferable to use a potential whose polarity is opposite to that of the ions being focused.
Simulation Of the Effects Of In-Homogeneous Grids
Fine mesh or grids are commonly used to establish and divide acceleration regions in TOFMS. When different electric fields are placed on each side of a grid, a small electrostatic lens is produced at each opening. The effects of these lenses on the ion throughput and time resolution of instruments has been a point of controversy. Two published papers have indicated that the grids have little or no impact on the performance of the instrument2,3. Others suggest that grids can have a considerable effect and in some cases may even be the limiting factor in instrument resolution4-6. We have used SIMION 3D v.6.0 to simulate the flight of ions through individual grid holes. This work is the continuation of a study by one of us (Colby) that was first attempted with SIMION v.1.2 in 1986.
The grid material most commonly used is produced by Buckbee Meers of St. Paul, MN. Their products include a wide variety of wire densities and transmissions. The most popular meshes have wire densities of 70, 117.6, 333, and 1000 lines per inch. These have optical transmission of 90.0, 88.6, 70.0,and 50 percent respectively.
Simulation Conditions
Our SIMION 3D simulation is illustrated in Figure 3. It included nine grid holes and the volume within a distance of 1.5 grid holes on either side of the grid. At that distance the electric field was assumed to be uniform and a pair of solid electrodes were used to establish the fields in either direction. (One of these electrodes has been removed in Figure 3 to view the grid more clearly.) After refining (SIMION's method of calculating the potentials of non-electrode points), the potentials of points on the boundary and those in the interior that should be the identical due to the symmetry of the grid surface were compared. This established that the number of grid openings in the simulation provided sufficient accuracy. We also moved the solid electrodes by small distances to establish that the volume of the simulation was satisfactory. The potentials at over 20 million grid points were used to calculate ion trajectories This was accomplished be specifying 5.1 million points and then employing two axis of symmetry. The grid and one electrode were held at ground while the other electrode was held at high potential in order to establish an electric field.
Fig. 3 - Simulated Section Of Grid
Ion Trajectories
Ions were flown under a variety of conditions. This included 70, 117.6, and 333 line per inch grids as well as electric fields of 2000 and 10,000 V/cm. Ions were also flown in both directions; e.g. from high field to field free region and visa versa. When ions originated in the field free region, they were assumed to start with 200 eV of energy. When flown in the opposite direction ions were assumed to have been accelerated through 1.0 cm to either 2000 or 10,000 eV of energy when they reach the grid. All trajectories started along the Z axis perpendicular to the surface of the grid.
Results
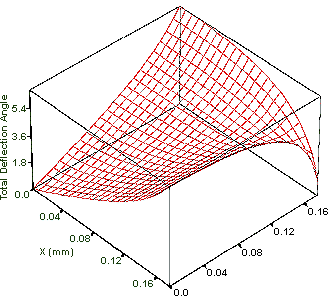
The profile of angular deflections due to passage through a grid opening is shown Figure 4. The X and Y axis are in distances relative to the center of the grid opening. This shape is typical of the results obtained. The area plotted represents one quadrant of the grid hole opening. In other quadrants the X and Y components of the deflection angle will have differing signs. The data displayed are for an ion traveling from a field free region into a 10,000V/cm field. The angle is measured relative to the Z axis at distance of only 0.55 mm after the grid. At this point an average of 6.3% of the total velocity is perpendicular to the original direction of flight (along the Z axis). If the region was only 0.55 mm long this would be the angle at which the ion reaches the next region. However, if the ion is accelerated further, i.e. from the current 744 eV to 10.2 KeV (1 cm travel) the deflection angle will be reduced dramatically because all of the additional velocity is in the Z direction. After this acceleration the average (absolute) deflection angle will be reduced from 3.62 to 0.99degrees.
Fig. 4 - Deflection Angles 0.55 mm After Passing Through a Grid
When the ions travel from a region of high electric field to a field
free region the deflection angle can be measured a short distance from
the grid since no further acceleration takes place. If we assume that all
ions start at rest and accelerate through the same distance before encountering
the grid then the results are independent of the acceleration field. The
difference in ion velocity are therefore compensated for by changes in
the electrostatic lens. Calculated results for a number of standard grid
sizes are shown in Table 1. These results are independent of ion
mass. The values for average deflection angle refer to the average absolute
value in a given quadrant. For each deflection angle one of opposite sign
is found in the opposite quadrant so the total average is zero.
Table 1: Deflection angles
Starting Region |
Grid Size |
Field Strength |
Deflection Angle.*,a |
Perpendicular Velocity *,a |
Deflection Angle.*,b |
Perpendicular Velocity*,b |
| Field Free | 70 (lines/inch) | 2000 (V/cm) | 2.33 (deg.) | 4.0 (%) | 0.91 (deg.) | 1.6 (%) |
| 117.6 | 2000 | 1.12 | 2.0 | 0.40 | 0.70 | |
| 333 | 2000 | 0.351 | 0.61 | 0.11 | 0.20 | |
| 70 | 10,000 | 3.62 | 6.3 | 0.99 | 1.7 | |
| 117.6 | 10,000 | 2.67 | 4.6 | 0.61 | 1.1 | |
| 333 | 10,000 | 2.58 | 4.5 | 0.45 | 0.80 | |
| High Field | 70 | any | 0.153 | 0.27 | 0.153 | 0.27 |
| 117.6 | any | 0.091 | 0.16 | 0.091 | 0.16 | |
| 333 | any | 0.033 | 0.058 | 0.033 | 0.058 |
*Average Values
aAt 1.5 times grid wire spacing.
bAfter 1.0 cm.
Ramifications In Real Instruments
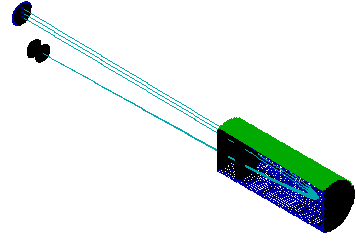
The angles listed in Table 1 are quite small, but we must consider their impact on real time-of-flight instruments. Consider a linear TOFMS with a single acceleration stage followed by a drift region and detector. In this example, with the worst case (0.153 degrees), an 18mm detector would have to be 3.3 meters from the source before 50% of the ions would be lost. So grid lensing does not appear to be a major problem for sensitivity although the change in time-of-flight is roughly proportional to the percent of perpendicular velocity (1.7%). A second example is shown in Figure 5. This reflectron includes a source, a two stage reflector, a detector, and two field free drift regions. The total length is 300 mm. Ninety percent of an ion's energy is removed in the first stage of the reflector. We observe the effects of ion lensing by simulating the trajectories of ions from the source to the detector. The figure shows three trajectories. One represents a non-deflected ion while the others indicate ion given angles of plus and minus 0.153 degrees at the exit of the source. Clearly ion scattering now has serious consequences for the performance of the instrument. With 70 lines per inch grids, the average ion falls 4 mm from the center of the ion beam. In addition, the flight time difference between the three ions is 25 ns! The difference between these two examples is that the reflectron has regions of deceleration. In these areas the velocity component due to deflection is unaffected so it becomes a greater fraction of the overall velocity. In the reflector this can quickly become the dominant component of velocity. For example, if the drift energy of undeflected 1000 amu ions is 2000 eV then the average ion will have velocity components of 52 and 19640 m/s after leaving the source. In the second stage of the reflector, the velocity along the long axis of the instrument is reduced from 19640 m/s to zero. During this time the 52 m/s velocity component perpendicular to the ion beam stays constant and has a considerable effect on the time of flight and the final position of the ion at the detector.
Fig. 5 - Reflectron Time-of-flight Mass Spectrometer.
Conclusions
SIMION 3D has been a useful tool for analyzing the problems of grid in-homogeneity in TOFMS. We have found that grids can indeed have a significant impact on the performance of time-of-flight instruments. This is particularly the case when ions experience decelerations as in a reflectron. Small deflection angles that are introduced when the ion is at high energy can have significant effects if the energy is reduced. Our results agree with the work of those who considered grids to be a considerable problem. The work of King, et al. Is perhaps the most thorough since they followed calculations with instrumental verification.
Future Work
The above simulations only consider the ramifications of a single grid. The cumulative effects of several deflections require a more sophisticated analysis. We are currently working on a SIMION 3D macro, using SIMION's user programming interface, that will allow the Monte Carlo simulation of ions passing through a series of grids.
References
- David A. Dahl 43ed ASMS Conference on Mass Spectrometry and Allied Topics, May 21-26 1995, Atlanta, Georgia, 717. (Software is distributed by Scientific Instrument Services, Ringoes, NJ.)
- X. Tang, R. Beavis, W. Ens, F. Lafortune, B. Schueler and K. G. Standing, Int. J. Mass Spectrom. Ion Processes, 85 (1988) 43.
- D. Ioanoviciu Int. J. Mass Spectrom. Ion Processes, 131 (1994) 43.
- T. Bergmann, T. P. Martin and H. Schaber, Rev. Sci. Instrum., 60 (1989) 347.
- R. C. King, R. Goldschmidt and K. G. Owens 39th ASMS Conference on Mass Spectrometry and Allied Topics, May 19-24 1994, Nashville, TN, 717.
- V.V. Laiko and A.F. Dodonov, Rapid Comm. Mas Spectrom. 8 (1994) 720-726.

